Synaptic

I found the “Mathematical Origami” paper written by Leland Schipper to be extremely interesting and very well written. In addition it seemed to offer an appealing topic for a broad audience, unlike many mathematical writings. It stood out as one of the better senior papers I had ever read.

-Tom Linton

---

---

The Japanese art of origami is not only fun and cool, but it is mathematically powerful too. Using only simple origami axioms and a little bit of creativity and time, we can fold truly amazing shapes. The possible applications of these origami shapes are just beginning to be explored. Origami is being used to create everything from massive space telescopes to tiny heart stints used in post heart attack surgery. The bounds of origami are being stretched and tested every day. The relationship between mathematics and origami has been around for centuries, but the exploration of this relationship and the use of origami to teach both lower and higher level mathematics is quickly growing. And while origami is being used increasingly often to teach mathematics, mathematics is also being used to prove a wide variety of theorems about origami. For instance, in this paper we will show how mathematics can be used to help us perform a flat vertex fold of a square using an interesting twist method. Applying mathematics to paper folding allows us to narrow down how many and what type of folds we should use to properly create flat folding models. At the same time, mathematics can also be used to do the opposite; it helps us explore how many different folds we can do – and just how far the limits of origami reach.

Before we explore the twist method for performing a flat vertex fold on a square, we are going to have to get a bit more familiar with origami, its guiding principles, and some key definitions. First, let’s begin with a definition of Origami.

Origami: The Japanese art of folding paper into decorative shapes and figures.

It is important to realize that this is an extremely broad definition of Origami. We will use a much more restricted view of Origami for the rest of this paper; We will abide by seven axioms. The first six were presented by Humiaki Huzita in 1991 and are referred to as Huzita’s Axioms, and the seventh axiom was written by Koshiro Hatori in 2001. These seven axioms are commonly accepted as the purest form of origami and we will use them to govern the ways in which we can fold paper in order to create origami forms. The seven axioms are as follows:

1.Given two points p1 and p2, there is a unique fold that passes through both of them.

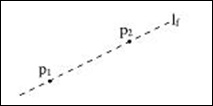
2.Given two points p1 and p2, there is a unique fold that places p1 onto p2.

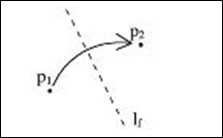
3.Given two lines l1 and l2, there is a fold that places l1 onto l2.

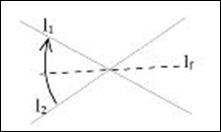
4.Given a point p1 and a line l1, there is a unique fold perpendicular to l1 that passes through point p1.

5.Given two points p1 and p2 and a line l1, there is a fold that places p1 onto l1 and passes through p2.

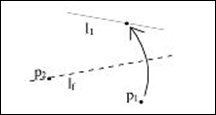
6.Given two points p1 and p2 and two lines l1 and l2, there is a fold that places p1 onto l1 and p2 onto l2.

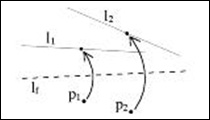
7.Given one point p and two lines l1 and l2, there is a fold that places p onto l1 and is perpendicular to l2.

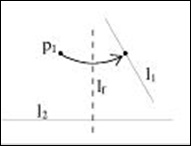
Given these seven axioms we can create millions of origami forms, but using only these axioms does restrict us in some ways. For instance, these axioms prevent us from using techniques like wet origami which allows us to create curved lines created by wetting the paper and molding the paper to create shapes impossible to create using pure origami techniques. It disallows the use of modular origami which allows for the combination and union of different pieces of paper into one origami form. And lastly, it prevents us from cutting the paper in any way which is allowed in a branch of origami called Kirigami.

There are multiple ways to display origami patterns, the most detailed of which is called an origami diagram. If you search for origami online and print off a pattern, you will usually be looking at an origami diagram. These diagrams not only show where you need to fold, but use numbered steps to sequence the moves. While these patterns are useful for novice folders, they are too difficult to create and use as origami gets more complicated. For this reason, most origami artists that use mathematics to achieve their creations use what is called an origami crease pattern. These patterns usually give you only two pieces of information, where folds occur, and what type of fold it is. There is no sequence provided with a crease pattern, and the author may choose to further limit information provided by the crease pattern by drawing all the lines the same so the user must discover for them self what type of fold is necessary. The following is an example of a crease pattern and its resulting origami creation.

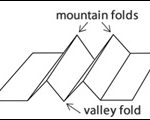As you can tell, this is a rather complicated crease pattern which would be nearly impossible to produce an exact sequence for. In order to properly fold this crease pattern you have to have a basic understanding of origami and some of the folding techniques. One of the keys to understanding a crease pattern is being able to distinguish between a mountain and a valley. A mountain fold is a crease that is concave downward so that the paper is folded away from you, resulting in the fold being nearest to you. A valley fold is its inverse: a crease that is concave upward so that the paper is folded towards you, resulting in the fold furthest from you. Both folds are displayed below.

Crease pattern authors use different lines to distinguish between mountains and valleys; from this point on in the paper, our crease patterns will differentiate between mountains and valleys using thin or dashed lines for valleys and bold lines for mountains.

One of the areas of Origami that has been studied recently with much intrigue is the concept of flat-foldability. Flat-foldability refers to the ability to fold the crease pattern of an origami model so that it lies completely flat using only our pure origami techniques. As mathematics has been applied to Origami in the last two decades, we have learned much in the field of flat-foldable shapes. In the remainder of this paper we will explore the possible crease patterns to perform a flat fold of a square twist crease pattern, which will entail flat folding at four vertices, but for now, let’s just analyze a single flat vertex fold to get an idea of how this works. If you look at figure 1 below, we can start to see some interesting properties of flat-foldability. For instance, for each fold in the circular crease pattern, we can either assign it a mountain fold or a valley fold. Therefore, we have a simple combinatorics problem that will tell us how many different ways we can fold this crease pattern. To solve this problem, we apply the Fundamental Counting Principle which states: if there are m ways to perform one task, and n ways to perform another, then there are mn ways to perform both tasks. Therefore, since in the fold below we have four creases to assign either a mountain or a valley folds, we have 24=16 possible origami models we can create from this single vertex crease pattern. It is important to note that most of these patterns will not actually fold flat. For example, if you have all mountain folds or all valley folds, it is impossible to fold the model flat without creasing it in places not indicated in the crease pattern.

Exploring the properties that govern flat foldability is a task that has been explored extensively as of late. The following four properties must hold true in order for a given single vertex crease pattern to be flat foldable.

1. The crease pattern must be two colorable. This is similar to the concept of the four color map problem, but instead of using four colors, we may only use two to make sure no two touching sections of our crease pattern are the same color. Below is an example of a two colorable crease pattern.

2. Kawasaki’s Theorem: Kawasaki’s Theorem : Given a vertex in a flat origami crease pattern, label the angles between the creases as α1, α2,… , α2n , in order. Then we must have: α1 + α3 +… + α2n-1 = α2 + α4 +… + α2n = 180°. Applying Kawasaki’s Theorem once again to Figure 1 on the previous page, we can conclude that in order for the model to be flat foldable, α1 + α3 = 180° and α2 + α4 = 180°.

3. Maekawa’s Theorem: Given a vertex in a flat origami crease pattern, if M is the number of mountain creases and V is the number of valley creases at the vertex, then we must have M-V=±2. For example, if we refer back to Figure 1 on the previous page, we can see how Maekawa’s theorem can be applied to a crease pattern. Since we have four creases, we cannot have all mountains or all valleys, or else we would be violating Maekawa’s theorem because the number of mountain and valley creases would differ by four. We also violate the theorem if we have two of each type of fold. Thus, the only valid choices we have are either three mountain folds and one valley fold, or three valley folds and one mountain fold.

4. A sheet may never penetrate a fold. In reality, with paper, a sheet could never actually penetrate a fold; instead, you would be forced to cut or tear the paper, or create folds not indicated on the crease pattern. This is basically the rule that prevents us from “cheating” while we fold our origami models. This property is actually pretty intuitive, and is the least technical of the properties, but is the most difficult to implement. The first three properties can easily be programmed and used to help solve foldability problems with the assistance of a computer. It is this last rule that the development of an algorithm has proven extremely tricky. There has been some progress in this field, and within the last decade computer scientists have co-opted with mathematicians to prove that assigning mountain and valley foldings in a crease pattern so that a sheet never penetrates a fold is equivalent to the logic problem that is computationally NP-complete. NP-complete logic problems could easily require a full course to understand the algorithms and programming necessary to solve them, but the important thing is that the leaders in the field of origami have found ways to use computers to solve flat foldability problems that the human mind could never fully process. One algorithm that is programmable and is a key element in solving these problems is the Big-Little-Big Angle Theorem which states: In a flat vertex fold if we have a sequence of consecutive angles αi-1 ,αi , and αi+1 with αi-1 > αi and αi < αi+1, then the two crease lines in between these three angles cannot have the same mountain-valley parity. This will be the only theorem we need later in this paper for our main result, but there are several more theorems and algorithms that help us uphold this fourth rule for all origami crease patterns.

Now that we understand the necessary elements to show that a single vertex crease pattern is flat foldable, let’s looks at a crease pattern which is undoubtedly more complex, and which has applications in both the artistic and practical realms of origami. This crease pattern is called a square twist because when folded, the paper “twists” into a smaller square; its crease pattern is given below without a mountain and valley assignment.

Not only does this origami model have many applications which we will discuss later, but it also is a great model to discuss some of the mathematics we can use to explore the flat foldability of crease patterns, and in a broader sense, to explore the limits of origami. The first thing you should notice about this crease pattern is that folding it flat will be much more difficult then folding a single vertex crease pattern. This pattern has four vertices, and at each vertex we must uphold the four fundamental rules of flat foldability. By design, the crease pattern already upholds the first two flat foldability rules. It is two colorable, and it upholds Kawasaki’s Theorem. Because our crease pattern, by design, upholds our first two rules, our goal is to use our last two rules, namely Maekawa’s Theorem and the Big-Little-Big Angle Theorem, to prove how many different assignments of Mountain and Valleys are possible while still remaining true to our axioms of origami and our four properties of flat foldability.

First, let’s look at the most basic assignment of mountain and valley folds for this crease pattern to get a better feel of what we are trying to do. The first figure on the following page is the crease pattern with the mountains determined by the bold lines and the valleys by the thin lines. The second figure is a representation of the origami model after we fold according to the crease pattern.

To better understand what we are trying to achieve, let’s start to consider how many ways we can assign mountain and valley folds to the square twist crease pattern. If we study the crease pattern above, we will find that there are twelve fold lines indicated on the crease pattern. Therefore, if we apply the fundamental principal of counting, considering that we have twelve fold lines to either assign a mountain fold or a valley fold, there are 212 or 4096 possible mountain and valley assignments. Luckily, that number is far larger than the number of unique flat foldable models. It over estimates for two reasons; first, that number accounts for all mountain and valley assignments you could possibly have, but many of those will break our third and fourth fundamental rules. For instance, one of the assignments out of the 4096 possibilities is a crease pattern with all mountain folds, but this doesn’t uphold Mawekawa’s theorem because the number of mountain and valley folds would differ by 12 instead of 2. The second reason 212 is an over-estimation is because there are a large amount of solutions that are not unique but instead represent a simple 90°, 180°, or 270° rotation of another solution. We will see some examples of these later. Therefore, to find the number of unique flat foldable solutions, we will have to find a way to weed out all these repetitions and non-flat foldable models.

First, let’s eliminate all the solutions that don’t uphold Maekawa’s Theorem and/or the Big-Little-Big Angle Theorem and therefore aren’t flat foldable. One way we could do this is by looking at all 4096 crease patterns and evaluating them individually to find which fail to uphold our fundamental rules. Proving this by exhaustion, however, would be, well, exhausting. Instead, if we study our square twist crease pattern, we can conclude that if we choose a mountain and valley assignment for two of the creases at each vertex, then we can apply the Big-Little-Big Angle theorem to tell us what assignment to give the third crease at each vertex. Then, once we have three creases at each vertex assigned, Maekawa’s Theorem will dictate the assignment of the fourth and final crease at each vertex. Therefore, all we really need to do is assign mountains and valley folds to two of the creases at each vertex. The easiest way to assign two creases at each vertex is to assign the four central folds that make up the diamond shape in the interior of the crease pattern. If we choose a mountain and valley assignment for these four folds in the diamond, we will have assigned two creases at each vertex, and thus, the rest of the creases in the pattern will be systematically assigned using our last two fundamental rules. The diagrams on the next two pages will help us explore how this systematic assignment happens when we apply Maekawa’s Theorem and the Big-Little-Big Angle Theorem.

Lets first assume our entire crease pattern is valley folds (determined by dashed lines here), and we are going to change some of them to mountain folds where appropriate. Next, let’s arbitrarily assign mountain and valley folds to the interior diamond. In the example below, I have assigned two mountain folds, so that folds j and m are mountains, while n and q remain valleys. This is just one example of many we could evaluate.

Let us first consider vertex B, and we will see how we can utilize our last two fundamental rules. At vertex B (and at every vertex) we have a situation where we can apply the Big-Little-Big angle theorem. The conditions of the theorem are met because the angle contained by the creases j and k is smaller than both angles surrounding it. Thus, we can use this theorem to establish that creases j and k cannot have the same mountain/valley parity. Since we have already assigned j a mountain fold, this means k must remain a valley fold as is already indicated. So now at vertex B we have three creases assigned: j and m are mountains, and k is a valley. Now we can apply Maekawa’s Theorem to determine the assignment of crease l. Since if we leave l as a valley as is currently indicated, our number of mountain and valley folds would differ by zero, we must assign l a mountain fold so that we have three mountains and one valley, and therefore, a difference of two. Thus, at vertex B, we have the following creases, which make it flat foldable at vertex B.

Now we can apply the same logic to vertex C, using the Big-Little-Big angle theorem to assign crease o a mountain fold. Then to uphold Maekawa’s theorem, we must assign crease p a mountain fold as well. Therefore, the model is now flat foldable at vertex B and C. If we continue to do this at each vertex, we get the following flat foldable crease pattern. We would have been able to apply these two theorems to systematically give a mountain and valley assignment to the outer eight creases no matter what we chose for our interior diamond.

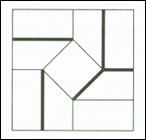We could have chosen to assign anywhere from zero to four mountains in the interior diamond, and we could have placed those assignments anywhere, and then we would be able to utilize our two theorems in the same fashion as demonstrated above.

Now that we understand that once we have selected the mountain and valley assignment for the interior diamond, the last two fundamental rules systematically assign all the folds as either mountains or valleys, we can throw out a majority of the 4096 possible assignments. Since there are only four creases in the interior diamond that we are choosing a mountain and valley assignment for, there are only 24 or 16 possible flat foldable solutions. But remember, there are still a sizable portion of these solutions that are not unique solutions, but instead, are rotationally symmetric to each other. For example, when we assign one mountain fold in the interior diamond, we could assign it to four different locations. These four possibilities are shown below.

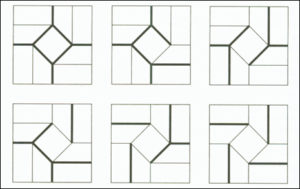If you look closely, you will notice that these four solutions are simply rotations of each other. If you had these four crease patterns in front of you, they would all be the exact same; it would just be a matter of how you were looking at it. Thus, there is only one unique solution with one mountain assignment in the interior diamond. In a similar fashion, there are four total solutions with three mountain assignments in the interior diamond, but only one of these is a unique solution. There are however, two different unique ways we can assign two mountain folds in the diamond. We can assign them adjacently, or opposite of each other. And lastly, there is exactly one way we can assign all mountains or no mountains in the interior diamond. Therefore, after throwing out all the rotationally symmetric solutions, there are only six unique ways of assigning mountains and valleys to the crease pattern to produce a flat foldable square twist. They are shown below starting with four mountains assigned in the interior diamond, then three, then the two ways to assign two, then one, and lastly, with no mountains assigned in the diamond. This model may seem somewhat trivial, but the square twist finds a solution to a fundamental question in the world of origami: How do we take a large object, fold it into a something smaller, and do so in a way that it takes a minimal number of forces to act upon it to return it to its original size. The square twist, once folded down, takes only two forces (a pull from any two corners) to expand it back to its regular size. On the other hand, if we had simply folded the paper in any manner we wanted to make it smaller, it would likely take several forces to act upon it to unfold it back to its original size. The square twist is also called a tessellation fold, meaning that it can be repeated several times so that we can take an arbitrary large crease pattern, and we can fold it down to a model that is as small as the material we are folding with will allow us to continue making folds.

The real world applications of folds like this are amazing. For example, a polygonal twist, much like the square twist we just looked at, is being used by Dr. Robert Lang to help send a telescope that is 100 meters in diameter into space. Because there is no room for a telescope of that size in a rocket, Dr. Lang is helping NASA utilize origami to fold the large lens in a manner such that it can fit into a rocket on earth, and then be easily expanded once in space.

Origami has been shown effective in applications that save human lives on a daily basis such as heart stents and airbags. Heart stents are used to hold arteries open in patients who have suffered a heart attack, and they fold down into very small capsules so that they can be strung through an artery and expanded once it reaches its destination. Car airbags also must be carefully folded so that they fit into very small spaces, but they must be folded in a way so that they can expand in a matter of milliseconds. Without using origami, the expansion of the airbag could take much longer because there would be several forces necessary to act upon the bag in order for it to properly expand.

The amazing thing about origami is that, compared to other fields of applied mathematics, it is still in its primitive years. We are only just beginning to explore the full potential of origami. New theorems are being discovered and utilized by computer science programmers every day to continue to push this field farther than anyone imagined. It is already being used to create beautiful artwork, see farther into space then we ever have, and to save countless lives, but who knows where it will take us in the future as we continue to use mathematics to explore its boundaries.

Works Cited

Hull, Thomas. Project Origami: Activities for Exploring Mathematics. Wellesley, MA: A K Peters, Ltd, 2006.

Hull, Thomas. “The Combinatorics of Flat Folds: a Survey.” The Proceedings of the Third International Meeting of Origami: Science, Mathematics, and Education. A. K. Peters; 2002.

Lang, Robert. Robert J Lang Origami. 2011. Web. 14 Nov. 2011. <http://www.langorigami.com>