Euclid’s Proof of the Pythagorean Theorem
By Katherine Lowe '18
MATH-386: Mathematics Seminar
Katherine’s paper is a very thorough exposition of Euclid’s proof of the Pythagorean Theorem. This proof is not seen very often outside an undergraduate Geometry course. Katherine tackled the proof with no prior undergraduate work in geometry. She worked to understand the material and then presented it logically and mathematically. Her explanations show complete understanding of the mathematical concepts and are detailed and clear. She uses complex and refined mathematical reasoning. She correctly uses terminology and notation throughout her paper (which is heavy on notation). Her paper is a stand-alone, mathematically easy to follow (for those with some experience reading proofs), and logical progression of Euclid’s proof of the Pythagorean Theorem.
–Wendy Weber
1. Abstract
This paper seeks to prove a significant theorem from Euclid’s Elements: Euclid’s proof of the Pythagorean theorem. The paper begins with an introduction of Elements and its history. Next, the paper establishes some foundational principles for Euclid’s proofs: definitions, postulates, and common notions. It then lists and explains some of the earlier propositions, which are needed to complete the later proofs. Then, Proposition I.47, the Pythagorean theorem, is proven, followed by Proposition I.48, its converse.
2. Introduction
One of the greatest works of mathematics is Euclid’s Elements; author William Dunham argues, of all the books ever written, “only the Bible has received more intense scrutiny” (30). Elements contained 465 propositions in 13 books, covering topics in both geometry and number theory. It should be noted that most of the theorems were not originally Euclid’s work, but he compiled the work of others and presented it in a “clear, organized, logical fashion” (Dunham 31). One of these propositions was Euclid’s proof of the Pythagorean theorem. Euclid was not the first to prove it, but this postulate, unlike many of the others, was entirely his own work. There have been hundreds of proofs of the Pythagorean theorem published (Kolpas), but Euclid’s was unique in both its approach and its organization, much like the rest of Elements. Written in 300 BC, Euclid’s Elements remains arguably the most important text on mathematics.
3. Postulates and Common Notions
Euclid began Elements with 23 definitions. He defined such things as a line, right angle, and parallel lines: “Parallel straight lines are straight lines which, being in the same plane and being produced indefinitely in both directions, do not meet one another in either direction” (Dunham 33). Notice that Euclid defined parallel lines as lines that never cross and not that they are everywhere equidistant, as is often done.
From here, Euclid introduced five postulates. These were self-evident statements built off the definitions; they did not need to be proven and were accepted as givens. Postulate 1 stated, “[It is possible] to draw a straight line from any point to any point” (Dunham 34). Another important postulate used in his proof of the Pythagorean theorem was Postulate 4: “All right angles are equal to one another” (Dunham 35). To anyone who has studied geometry, these statements are undeniable, which is exactly what Euclid intended.
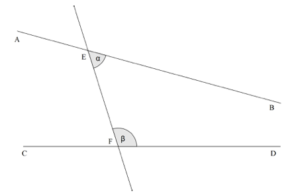
Figure 1: Postulate 5
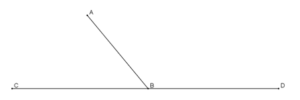
The most controversial aspect of Euclid’s Elements was Postulate 5. It stated, “If a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles” (Dunham 35). In other words, if α + β is less than two right angles, lines AB and CD cross at some point (Figure 1). This postulate was far more complex and less obvious than the previous ones; many mathematicians felt that this was really a theorem and should not be assumed true. Euclid, understanding this sentiment, avoided using Postulate 5 in his propositions. He did not use it at all in the first 28 propositions.
Following the Postulates, Euclid introduced five common notions. Like the postulates, these were accepted facts that did not need to be proven; however, the common notions were “of a more general nature, not specific to geometry,” unlike the postulates (Dunham 36). Common Notion 1 was the equivalent of the transitive property of addition: “Things which are equal to the same thing are also equal to one another” (Dunham 36). Common Notion 2 stated, “If equals be added to equals, the wholes are equal” (Dunham 36). In algebraic terms, if a = b, then a + c = b + c.
4. Other Propositions
In order to prove the Pythagorean theorem, Euclid used conclusions from his earlier proofs. We will consider the propositions needed to prove this and other theorems.
- Figure 2: Proposition I.4
- Figure 3: Propositions I.13 and I.14
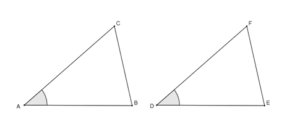
Proposition I.4 proved the congruence of two triangles; it is commonly known as the side-angle-side theorem, or SAS. Euclid proved that “if two triangles have the two sides and included angle of one respectively equal to two sides and included angle of the other, then the triangles are congruent in all respect” (Dunham 39). In Figure 2, if AC = DF, AB = DE, and ∠CAB = ∠FDE, then the two triangles are congruent. This means that not only are the remaining sides and angles congruent, but the two triangles also have the same area.
In Proposition I.8, Euclid proved another congruence theorem. If two triangles have all three sides of one triangle equal to all three sides of the other triangle, the triangles are congruent. This is called the side-side-side theorem, or SSS.
Euclid showed how to construct a line perpendicular to another line in Proposition I.11. He showed that this line could be drawn from a point on the line or a point not on the line. This proposition was one of many construction proofs. Proposition I.14 considered when a line is straight. In I.13, Euclid showed that if line CBD in Figure 3 is a straight line, then the angles ∠CBA and ∠ABD sum to two right angles.
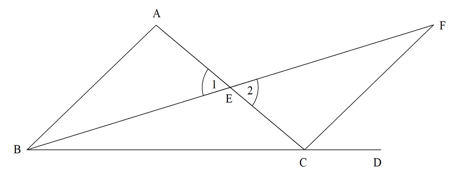
Figure 4: Proposition I.16
Proposition I.14 is the converse of this: if ∠CBA and ∠ABD sum to two right angles, then line CBD is a straight line. Proposition I.16 states, “In any triangle, if one of the sides be produced, the exterior angle is greater than either of the interior and opposite angles” (Dunham 41). That is, in Figure 4, ∠DCA is greater than ∠CBA or ∠BAC. To prove this, Euclid bisected the line segment AC with line BF, where BE = EF. He then drew line segment FC. Since AE = EC by the bisection, BE = EF by construction, and ∠1 = ∠2 (since vertical angles are equal), we see that ΔAEB and ΔCEF are congruent by SAS, Postulate I.4. Clearly, ∠DCA is larger than ∠FCE, and since ∠FCE = ∠BAE, ∠DCA is larger than the interior angle ∠BAC. By a similar argument, Euclid showed that ∠DCA was also larger than interior angle ∠CBA.
In Proposition I.27 Euclid proved that “if a straight line falling on two straight lines make the alternate angles equal to one another, the straight lines will be parallel” (Dunham 44). Given that angles 1 and 2 in Figure 5 are equal, he assumed lines AB and CD intersected at point G and looked for a contradiction. In a triangle, according to Proposition I.16, the exterior angle ∠2 is greater than either interior angle. However, since ∠1 = ∠2, we have a contradiction. Therefore, lines AB and CD never intersect and are, by definition, parallel.
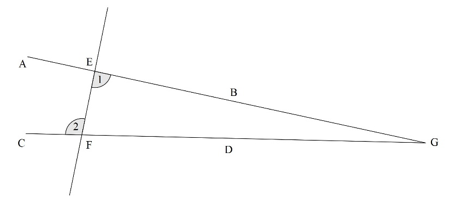
Figure 5: Proposition I.27
Another construction proof was given in Proposition I.31. Here, Euclid showed how to construct a line parallel to a given line through a point not on the given line.
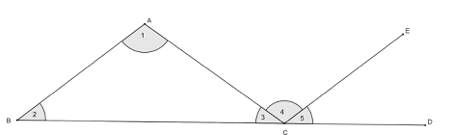
Figure 6: Proposition I.32
Proposition I.32 is a well-known fact of geometry: the three interior angles of any triangle sum to two right angles. In Figure 6, Euclid constructed line CE parallel to line BA. Therefore, ∠1 was equal to ∠4, and ∠2 was equal to ∠5, as shown in Proposition I.29. So, the sum of the interior angles of ΔABC was: ∠1 + ∠2 + ∠3 = ∠4 + ∠5 + ∠3 = 2 right angles.
This equation is true because line BCD is a straight line, which is equal to two right angles by Proposition I.14 (Dunham 46).
In Proposition I.41 Euclid proved the equivalent of the equation A = ½bh, for the area of a triangle. He showed that if a triangle and a parallelogram share the same base and fall between the same parallel lines (i.e. have the same height), then the area of the parallelogram is twice the area of the triangle. In Figure 7 the triangle and parallelogram share the base line segment AB and fall between the parallel lines AB and CD. According to Proposition I.41, the area of the triangle is half the area of the parallelogram.
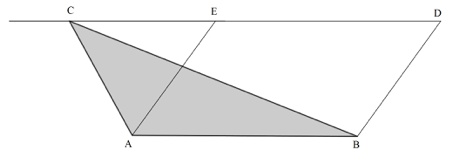
Figure 7: Proposition I.41
The last theorem Euclid needed in order to prove the Pythagorean theorem was Proposition I.46. Here he showed how to construct a square from a given line segment. The next proposition was his proof of the Pythagorean theorem.
5. Proposition I.47
Theorem: In right-angled triangles, the square on the side subtending the right angle is equal to the squares on the sides containing the right angle (Dunham 48).
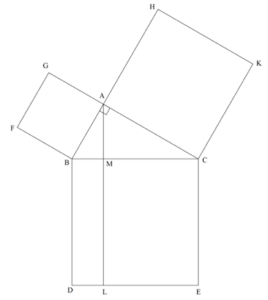
Unlike the typical algebraic understanding of the Pythagorean theorem as a² + b² = c², Euclid constructed actual squares BCED, ABFG, and ACKH from the sides of the right triangle ΔABC using Proposition I.46 (Figure 8). This shape came to be called “the windmill” as Euclid’s proof gained popularity. Euclid sought to prove that the area of BCED was equal to the sum of the respective areas of ABFG and ACKH.
- Figure 8: “The Windmill”
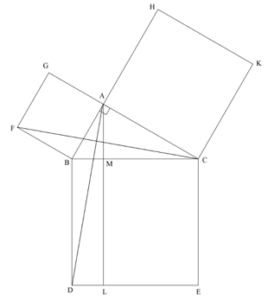
- Figure 9: Triangles ΔABD and ΔFBC
Euclid employed Proposition I.31 to draw line AL through A parallel to line BD. From here, Euclid sought to prove that the area of square ABFG was equal to the area of rectangle BDLM, and the area of square ACKH was equal to the area of rectangle CELM. To show that line segments CA and AG were on the same straight line, Euclid noted that ∠BAC was a right angle by the hypothesis and ∠GAB was a right angle by the construction of the square. Thus, the two angles sum to two right angles; by Proposition I.14, line CG is a straight line.
Using Postulate 1, Euclid drew line segments AD and FC, forming triangles ΔABD and ΔFBC (Figure 9). Since they are sides of the same square, AB is equal to FB by construction. Likewise, BD = BC. We see that: ∠ABD = ∠ABC + ∠CBD = ∠ABC + (right angle)
Similarly, ∠FBC = ∠ABC + ∠FBA = ∠ABC + (right angle)
Therefore, by Postulate 4, which states that all right angles are equal: ∠ABD = ∠ABC + (right angle) = ∠FBC
By Proposition I.4, which proved the side-angle-side theorem, ΔABD and ΔFBC are congruent since AB = FB, BD = BC, and ∠ABD = ∠FBC. Using Proposition I.41, Euclid observed that the area of ΔABD and rectangle BDLM shared the base line segment BD and fell between the parallel lines BD and AL. Thus, Area (rectangle BDLM) = 2 Area (ΔABD)
Similarly, ΔFBC and square ABFG share base line segment BF and fall between parallel lines BF and CG, since we have shown CG is indeed a straight line. So, Area (square ABFG) = 2 Area (ΔFBC)
We have already shown ΔABD and ΔFBC are congruent by SAS, so we can conclude: Area (rectangle BDLM) = 2 Area (ΔABD) = 2 Area (ΔFBC) = Area (square ABFG)
Therefore, Area (rectangle BDLM) = Area (square ABFG)
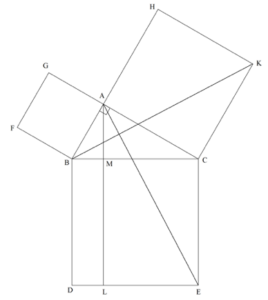
Figure 10: Triangles ΔACE and ΔKCB
Euclid was half-way done with his proof. Next, he followed a similar method to show the area of square ACKH was equal to the area of rectangle CELM. He drew segments AE and BK to form triangles ΔACE and ΔKCB (Figure 10). Since ∠BAC is a right angle by hypothesis, and ∠CAH is right by construction, ∠BAH sums to two right angles, and, by Proposition I.14, line BAH is a straight line.
Next, Euclid showed ΔACE was congruent to ΔKCB. Sides AC and CK are two sides of the same square, and thus the lengths are equal. Similarly, BC and CE are equal. He then proved ∠KCB = ∠ACE: ∠KCB = ∠BCA + ∠ACK = ∠BCA + (right angle) Also, ∠ACE = ∠BCA + ∠BCE = ∠BCA + (right angle) Therefore, ∠KCB = ∠BCA + (right angle) = ∠ACE
Since ΔACE and ΔKCB have two sides and their interior angles are equivalent, ΔACE is congruent to ΔKCB by SAS.
Returning to Proposition I.41, Euclid observed ΔACE and rectangle CELM share base CE and fall between parallel lines CE and AL. Thus, Area (rectangle CELM) = 2 Area (ΔACE)
Also, ΔKCB and square ACKH share base CK and fall between parallel lines CK and BH, since we have already proven line BH is a straight line. Thus, Area (square ACKH) = 2 Area (ΔKCB)
Since ΔKCB and ΔACE are congruent, their areas are equal: Area (rectangle CELM) = 2 Area (ΔACE) = 2 Area (ΔKCB) = Area (square ACKH)
Therefore, Area (rectangle CELM) = Area (square ACKH)
Finally, since Area (square BCED) = Area (rectangle BDLM) + Area (rectangle CELM)
by construction, we have: Area (square BCED) = Area (rectangle BDLM) + Area (rectangle CELM) = Area (square ABFG) + Area (square ACKH)
So, we see that the area of the square on the side opposite the right angle is equal to the sum of the areas of the squares on the other two sides. Euclid’s proof is complete.
6. Proposition I.48
While the Pythagorean theorem is well-known, few are familiar with the proof of its converse. Euclid immediately followed Proposition I.47 with the proof of the converse of the Pythagorean theorem in I.48.
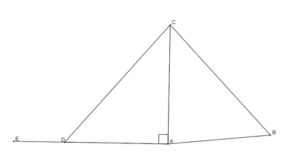
Figure 11: Proposition I.48
Theorem: If in a triangle, the square on one of the sides be equal to the squares on the remaining two sides of the triangle, the angle contained by the remaining two sides of the triangle is right.
From the hypothesis, Euclid constructed ΔABC, assuming BC² = AB² + AC² (Figure 11). He then showed ∠BAC was a right angle. He drew line segment AE perpendicular to AC, using Proposition I.11. Then he constructed AD = AB and connected D to C with line segment CD. Now he had two triangles: ΔBAC and ΔDAC.
The triangles share side AC, and AD = AB by construction. Because line segments AC and AE are perpendicular, ∠DAC must be a right angle. By the Pythagorean theorem, CD² = AD² + AC²
Substituting AD = AB, CD² = AD² + AC² = AB² + AC²
From our hypothesis, CD² = AB² + AC² = BC²
Because CD² = BC², CD must equal BC. Since all three sides are equal in length, ΔBAC and ΔDAC are congruent by SSS, Proposition I.8. But if they are congruent, then ∠DAC = ∠BAC, so ∠BAC must be a right angle. Thus, the converse of the Pythagorean theorem is proved.
7. Conclusion
Euclid’s proof of the Pythagorean theorem is only one of 465 proofs included in Elements. Unlike many of the other proofs in his book, this method was likely all his own work. His proof is unique in its organization, using only the definitions, postulates, and propositions he had already shown to be true. Euclid’s proof takes a geometric approach rather than algebraic; typically, the Pythagorean theorem is thought of in terms of a² + b² = c², not as actual squares. The other propositions in Elements contain the same level of organization, clarity, and ingenuity of Propositions I.47 and I.48. Euclid’s Elements is a mathematical masterpiece well-deserving of the attention it receives.
Works Cited
Dunham, William. “Euclid’s Proof of the Pythagorean Theorem.” Journey Through Genius: The Great Theorems of Mathematics. New York: Wiley Science Editions, 1990. 27-60. Print.
Kolpas, Sid J. “Mathematical Treasure: James A Garfield’s Proof of the Pythagorean Theorem.” Mathematical Association of America.
Mathematical Association of America, 2016. Web. 9 April 2017.