
Complex Ion composition determination by Job’s method
By Noel Powell '93
Inorganic Chemistry
Writing Objective: Laboratory Report
The composition of the complex ion nickel(II) ethylene-diamine, Ni(NH2CH2CH2NH2)x. in aqueous solution, is determined by the method of continuous variations, or Job’s method.
Often in inorganic chemistry, two or more species can interact to form a complex that cannot be isolated as a stable compound. In this case, the composition of the complex must be determined by other methods. One such method, the Job’s method, is concerned with evaluating n for the equilibrium below. In this experiment Z is Ni2+ and L is the ligand ethylenediamine (en).
![]()
Experimentally, the absorption at a given wavelength of a series of solutions containing varying molar fraction of Z and L is measured. If the equilibrium lies far to the right in equation (1), then the absorption will be greatest when the [L] in the solution Is exactly n times greater than [Z]. Therefore, we can determine n and thus the composition of ZL„ by knowing the ratio of L to Z in the solution that contains a maximum absorbance of ZLn.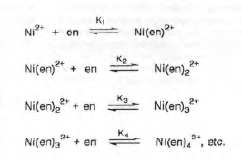
Depending on the value of the equilibrium constants, certain species will predominate in solution.
The theory behind the Job’s method is that if the absorbance at a given wavelength of each solution is plotted against the mole fraction of the ligand, the maximum absorbance will occur at a mole fraction that corresponds to the composition. Equimolar solutions of Z and L, each of M moles/liter, are mixed in varying amounts, so that the total (Z and L) Is M. A series of these solutions may be prepared by the addition of X liters of L to (1-X) liters of Z. The concentrations of Z, L and ZLn at equilibrium are as follows,
where K is the equilibrium constant for the reaction (1). Since the condition of a maximum in a curve of [ZLnl verses X is that we can differentiate equations (2), (3), and (4) with respect to X and combine the differential equations with equations (2), (3), and (5) to yield.![]()
Now we must determine the mole fraction X at which the absorbance of (ZLn] is a maximum. Since the absorbance of a solution is the sum of the absorbances of the species present, we can write,![]()
where e = molar extinction coefficient of each species and 1 = path length of the cell. If there Is no Interaction between Z and L ([ZLn] = 0) then the absorbance would be.
![]()
The difference between Ameas and AZ+L Is denoted as Y Where Az is the absorbance of the pure M molar N12+ solution.![]()
If we plot Y vs. X at a given wavelength we can find the maximum absorbance that occurs at a certain mole fraction. Since the different Ni(en)2+ complexes have different extinction coefficients, we can determine all of the different complexes present In solution.
Experimental
An aqueous solution of 0.4 M N1SO4.6H20 was made by dissolving 10.51 g N1SO4.6H20 In 100 mL deionized water. likewise, an aqueous solution of 0.4 M ethylenediamine was prepared by diluting 2.67 mL ethylenediamine to 100 mL deionized water. Seven solutions with various mole fractions of ethylenediamine and a total volume of 10 mL were prepared by diluting 3, 4, 5, 6, 7, 8, and 9 mL of the ethylenediamine solution to 10 mL with the N1S04 solution to form solutions with respective mole fractions of ethylenediamine of 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, and 0.9. The absorbances of each solution and the pure NIS04 solution were measured against deionized water at 530, 545, 578, 622, and 640 nm. The results are shown In Table 1.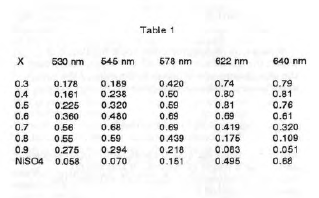
The Y values were then calculated from equation (7). These are shown in Table 2.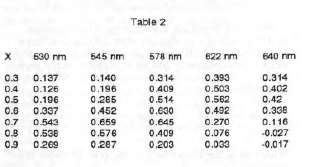
These values were plotted against the mole fraction of ethylenediamine (Graphs 1-5). The slopes on each side of the maximum were triangulated to find the maximum absorbance. Table 3 shows the mole fraction at which maximum absorbance occurred for each wavelength and the results of using the X values in equation (6).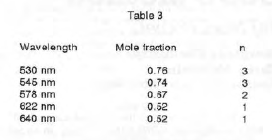
Thus I conclude that there are three species existing in equilibrium in these solutions, Ni(en)2+, Ni(en)22+, and Ni(en)32+.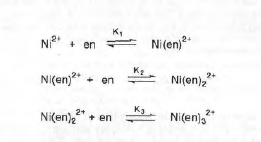
It is known that Ni2+ prefers to form octahedral complexes due to its d8 electron configuration. However, the presence of the relatively strong field ligand ethylene-diamine, enables the square planar complex to also be formed. The proposed structures of the complexes are shown in Figure 1. Although I believe this lab to be fairly accurate, there Is one particular source of error I would like to point out. The ethylenediamine used in this experiment had oxidized over time in the bottle, as the solution was a light brown in color. In future experiments, I would suggest distilling the ethylenediamine to obtain a pure ligand.